
Профессор информатики Брент Йорги в всоём блоге рассказал о том, как смог шестилетнему сыну доступно объяснить университетский материал. Предлагаем перевод его колонки.

Вчера ко мне подошёл мой шестилетний сын и спросил:
— А что ты читаешь?
Читал я на тот момент одну из глав докторской диссертации Джениса Воигтлендера. Даже не зная, с чего начать, я решил ответить прямо:
— Я читаю очень длинную сказку о свободных теоремах.
Но ему этого было недостаточно:
— А что такое свободные теоремы?

Так как перед педагогическими задачками я никогда не робел, то, немного поразмыслив, начал:
— Ты знаешь, что такое функция? (Он не знал.) Функция — это как машина, в которую ты помещаешь что-то с одной стороны, а с другой выходит что-то новое. Например, ты можешь ввести число, а выйдет из неё число, которое на один больше. То есть если ты введёшь 3, то выйдет 4, а если введёшь 6 — выйдет 7.
Я видел, что он действительно всё понимает, и продолжал:
— Тип такой функции показывает, какие именно вещи нужно вводить и какие мы получим на выходе. Можно вводить число и на выходе получить число. Или вводить список чисел и получать список чисел.
Он живо подхватил:
— Или, может, можно вводить слова?
— Точно! Можно вводить слова и получать тоже слова. Существуют даже функции, в которые можно вводить другие функции и на выходе получать тоже функции!
Сына идея помещать функции в функции привела в восторг. Я подытожил:
— Так вот, свободная теорема — это когда ты можешь сказать что-то, что всегда верно для функции, если ты знаешь только её тип, но не знаешь ничего о том, что она делает внутри.
Похоже, это было для него уже слишком (и если честно, свободные теоремы интересно разбирать только вместе с полиморфизмом, которого я, естественно, касаться не хотел). Но весь этот диалог натолкнул меня на кое-какую мысль.
— Послушай, я придумал занятную игру. Она называется «игра в функции». Я загадаю функцию. Ты будешь говорить мне, что мы будем в неё вводить, а я буду говорить, что получается на выходе. А потом ты будешь отгадывать, что делает эта функция.

Игра ему сразу понравилась, и настолько сильно, что играть в неё он готов без остановки: мы играли, пока вчера ехали в гости, сегодня утром пока я принимал душ. Вот что ему уже удалось угадать:
- x. x + 1
- x. x – 3
- x. 10x
- x. 2x
- x. 6
- x (слово). слово во множественном числе.
- x. 10 [x/10]
Я попробовал x. –(x + 2) и x. –(x + 10), но для него это было сложновато. Я заметил, что в некоторых случаях он внутренне понимал, что делает функция, но не мог выразить это словами (так было, например, с функцией x. 10 [x/10]). Поэтому мы немного изменили правила: когда отгадывающий думал, что знает, что делает функция, мы менялись ролями. Загадывающий функцию теперь придумывал вводные, а разгадывающий должен был подсчитать правильный ответ с этой функцией.
На удивление трудной для него оказалась функция x. 6 (хотя в итоге он с ней всё-таки справился). Думаю, он просто зациклился на том, что функция обязательно должна давать число, отличающееся от вводимого, и поэтому безуспешно пытался найти такую, которая при любых условиях на выходе даёт 6. Его просто смутило, что машине может быть всё равно, какие вводные она получила. (Любопытно, что многих студентов моего курса по функциональному программированию тоже часто сбивали с толку константные функции, когда мы проходили лямбда-исчисление. Им казалось, что вводные обязательно должны меняться, и приходили в замешательство от того, что в теле функции вообще отсутствует связанная переменная).
Несколько раз отгадав мои функции, он захотел придумывать их мне сам (как я и ожидал). Иногда они действительно были здоровские, а иногда немного бессмысленными (обычно потому, что он на ходу изменял их, но, конечно же, признавать ни в какую не хотел). И когда он наконец понял функции x. –(x + 2) и x. –(x + 10), то придумал свою, которая была похожа на
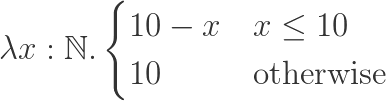
Думаю, на это его вдохновило занятие в садике, на котором они изучали пары цифр, которые в сумме дают 10. Это точно один из моих лучших дней с сыном.





Релоцировались? Теперь вы можете комментировать без верификации аккаунта.